Numbers

Now, suppose you have a younger sibling who has eaten the top-left square of your chessboard. Can you completely cover without overlap this chessboard with $2 \times 1$ dominoes?

What if they also ate the bottom-right square? Does this change your answer?

Now, we know that this isn’t right, and that $\dfrac{1}{x} + \dfrac{1}{y}$ is actually $\dfrac{y}{xy} + \dfrac{x}{xy} = \dfrac{x+y}{xy}$ . Sometimes, however, even a formula that is wrong in general might be right in a specific situation! Think of the old adage “a stopped clock is right twice a day”.

Does this ever happen with this mistake? In other words: are there any values $x,y$ such that $\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{x+y}$ ? Or is this false for literally every value of $x$ and $y$ ?

Integers

We start our coursebook by studying the integers! In case you have not seen the word “integer” before, we define it here:

The symbol $\mathbb{Z}$ comes from the German word “Zahl”, which means “number”, in case you were curious.

Example 1.1. The numbers $1, -7, 10000, 78, 45, 0, -345678$ are integers, but things like $\sqrt{2}, -2.787878787, \frac{1}{8}$ and $\pi$ are not.

In some form or another, integers have been used by humans for almost as long as humans have existed theirselves. The Lebombo bone, one of the oldest human artifacts, is a device on which people used tally marks to count the number of days in the lunar cycle. The base-10 system and idea of numerals took a bit longer for us to discover, but we can trace these concepts back to at least the Egyptians and Sumerians around 4,000-3,000 BC. Finally, negative numbers and zero have been with us for at least two millenia: historical documents tracking back to at least 1000 BC describe how Chinese mathematicians used negative numbers solve concrete problems on bounding areas of fields, exchanging commodities, and debt.

In short, integers are quite handy! To this day, we use them to model all sorts of problems. To give a pair of examples, let’s solve the first two exercises from this chapter:

Answer to Exercise 1.1. By just trying things out by hand, it’s relatively straightforward to find a tiling of a $8 \times 8$ board with no squares missing; one solution is drawn below.

When you remove a square, however, things get a bit more interesting! Try it for a while; no matter how you do this, you’ll always have at least one square left over uncovered.

However, saying “I tried it a lot and it didn’t work” is not a very persuasive argument. Suppose that you had a boss that said that Chad from Marketing said this was totally possible, and to have a working version on their desk by 5pm or you’ll be fired. What do you do?

Well, maybe you start revising your resumé and looking for other work. Before that, though, you may want to try to make a logical argument to your boss that shows that it’s impossible to come up with such a tiling - a set of reasons so airtight that no matter what they think or would respond with, they’d have to agree that you’re right. In mathematics and computer science, we call such logical arguments proofs!

In this class, we’re going to write these kinds of arguments for almost all of the claims that we make. We’re going to leave the rules for what constitutes a “proof” a little vague at first; in our first few chapters, we’re going to just try to write a solid argument that tells us why something is true, and anything that does that we’ll count as a proof. (Later in this course, we’ll approach proofs a bit more formally: feel free to read ahead if you can’t wait!)

For this problem, let’s prove that an $8 \times 8$ chessboard without a single square cannot be covered with $2 \times 1$ dominoes as follows:

Proof.

First, notice that each time we place a $2 \times 1$ domino on a board, it covers two squares worth of area. Because dominoes cannot overlap, this means that if we have placed $k$ dominoes on our board, there are $2 k$ squares of our board covered by dominoes.

If we have an $8 \times 8$ chessboard that’s missing a square, that board has $8 \cdot 8 - 1 = 63$ squares on it in total. Therefore, if we’ve completely covered our chessboard with dominoes, the number $k$ of dominoes we used must satisfy the equation $2k=63$ .

In other words, we have $k=31.5$ ; i.e. we’ve used half of a domino! This means that the other half of that domino is sticking off of our board or overlaps another domino, which means we’ve broken the rules of our tiling problem. So this is impossible! $\Box$

Notice how in the argument above, the only things we used were factual observations (i.e. the number of squares in our $8 \times 8$ grid minus a square, the amount of area taken up by each $2 \times 1$ domino) and logical combinations of those observations. This is how you write a solid argument!

To get a bit more practice with this sort of thing, let’s try the last part of our exercise. In this problem, we had a chessboard with its top-left and bottom-right squares removed, and wanted to try to cover this with $2 \times 1$ dominoes.

On one hand, the argument above no longer tells us that this is impossible. A $8 \times 8$ board minus two squares contains 62 squares in total; therefore, it might be possible to do this with 31 dominoes! However, if you try this for a while, you’ll find yourself quite stuck again. So: why are we stuck? What is a compelling argument we could write that would persuade someone that this is truly impossible, and not just that we’re bad at tiling?

After some thought and clever observations, you might come up with the following:

Proof.

1. Notice that each time we place a $2 \times 1$ domino on our grid, it’s not just true that it covers two units of area: it also covers exactly one unit of white area and one unit of black area! This is because our chessboard has alternating white and black squares.

2. Because dominoes cannot overlap, this means that if we have placed $k$ dominoes on our board, there are $k$ white squares and $k$ black squares covered by our dominoes. In particular, this means that we always have as much black area covered as white area!

3. However, if we count the black and white area in our $8 \times 8$ board with the top-left and bottom-right squares removed, we can see that there are 32 black squares and 30 white squares. These numbers are different! Therefore, it is impossible to cover this board with dominoes as well.

Notice that when we wrote this argument, we used observations from our earlier work, and modified them to suit this new problem! This is a good problem-solving technique in general: always see if you can modify a pre-existing solution before trying to come up with something entirely new.

In our working above, the fact that we could not write 63 as an integer multiple of 2 was a very useful observation! We can generalize this into the concepts of even and odd integers:

Even and Odd Integers

Example 1.2. 2 is even, because we can write $2 = 2 \cdot 1$ , and $1$ is an integer. Similarly, $4$ is an even number, because we can write $4 = 2 \cdot 2$ and $2$ is an integer.

As well, $-2, -4$ and $-6$ are all even, because we can write $-2 = 2 \cdot (-1)$ , $-4 = 2\cdot (-2)$ and $-6 = 2 \cdot (-3)$ , where $-1,-2,-3$ are all integers.

3 is odd, because we can write $3 = 2+1$ and 2 is even (as shown above.) Similarly, because $5 = 4+1$ and $7=6+1$ , we have that 5 and 7 are also odd. As well, $-1, -3, -5$ are all odd, as $-1 = -2 +1, -3 = -4+1,$ and $-5 =-6+1$ .

To get some practice writing logical arguments, let’s look at a few properties of even and odd numbers that you already know:

Claim 1.1. The sum of any two odd numbers is even.

Before getting into a “good” solution for this claim, let’s first study an argument that doesn’t work.

“Bad” solution: Well, $1+1 = 2$ is even, $3+7 = 10$ is even, $-13 + 5 = -8$ is even, and $1001 + 2077 = 3078$ is even. Certainly seems to be true! $\Box$

A defense of the “bad” solution: This might seem like a silly argument, but suppose we’d listed a thousand examples, or a billion examples, or set a computer program to work overnight and had it check all of the pairs of numbers below $10^{12}$ . In many other fields of study, that would be enough to “show” a claim is true! (Think about science labs: there, we prove claims via experimentation, and any theory you could test a billion times and get the same result would certainly seem very true!)

Why this argument is not acceptable in mathematics and computer science: When we make a claim about “any” number, or say that something is true for “all” values, we want to really mean it. If we have not literally shown that the claim holds for every possible case, we don’t believe that this is sufficient!

This is not just because computer scientists are fussy. In the world of numbers, there are tons of “eventual” counterexamples out there:

• Consider the following claim: “The sequence of numbers ”$12, 121, 1211, 12111, 121111, \ldots$ ” are all not prime.”

If you were to just go through and check things by hand, you’d probably be persuaded by the first few entries: $12 = 3\cdot 4, 121 = 11 \cdot 11, 1211 = 173 \cdot 7, 12111 = 367 \cdot 11, 12111 = 431 \cdot 281, \ldots$

However, when you get to $12\overbrace{111\ldots1}^{136~1's}$ , that one’s prime! This is well beyond the range of any reasonable human’s ability to calculate things, and yet something that could come up in the context of computer programming and information security (where we make heavy use of 500+ digit primes all the time.)

Here’s a fun exercise one of the writers of this coursebook saw in the wild on Facebook, shared by one of our troll-ier friends:

On its surface, this looks simple, right? Just solve it.

And yet: suppose you set a computer program to work at this problem, by just bashing out all possible triples of numbers. To be fair, let’s give you access to the world’s fastest supercomputer. By the end of a week, you wouldn’t have found an answer. By the end of a year, you wouldn’t have found an answer! Indeed: by the time we reached the heat death of the universe, you’d still have found nothing. You’d be tempted to say that no answer exists, right?

And yet, an answer exists! The math required to find this goes way beyond the scope of this course, but if you’re curious: the smallest known answer is to do the following:

In general, mathematics and computer science is full of things like this! Huge numbers that are prime or that satisfy equations similar to the ones above can be incredibly useful in information security (as you’ll see in later papers in Compsci/Maths!)

Examples alone, then, are not enough for a good argument. What would a good solution look like here? Here is one of many possible answers:

Proof.

Take any two odd numbers. Let’s give them names, for ease of reference: let’s call them $M$ and $N$ . By definition, because $M$ and $N$ are odd, we can write $M = 2k+1$ and $N = 2l+1$ , for two integers $k, l$ .

Therefore, $M+N = (2k+1) + (2l+1) = 2k+2l + 2 = 2(k+l+1)$ . In particular, this means that $M+N$ is an even number, as we’ve written it as a multiple of 2!

The argument above might look a little awkwardly-written to you at a first glance! This is because mathematics is something of a language in its own right: there are certain phrases and constructions with very specific meanings in mathematics, that we use when making arguments to ensure that they’re completely rigorous. Let’s talk about some of those phrases and concepts that came up in the argument above:

• We worked in general! That is, we didn’t just look at a few examples, but instead considered arbitrary values! This is what writing a phrase like “Take any two odd numbers” does for us: it doesn’t lock us into specific odd numbers, but instead tells the reader that we’re going to show that this works for anything that could ever come up.

• We defined our variables! That is, we didn’t just try to use pronouns to refer to our odd numbers the whole way through: instead, we gave them variable names, by calling them $N$ and $M$ . This makes writing our arguments much cleaner, as it’s much easier to refer to something if it has a name!

Note also that we defined these variables only after saying what kind of object they were! This is like when you’re writing code: you typically have to declare the type of variable you’re working with, i.e. you’d write something like int numA instead of just saying numA.

• We used words to describe what we were doing and why it worked! Mathematics, surprisingly, has a lot of words and sentences in it. You should find that the number of sentences in most solutions you make in this class exceeds the number of equations!

To get a bit more practice with this, let’s try out a few more claims:

Proof.

As before, let’s start by taking any two odd numbers. Let’s give them names, and call them $M$ and $N$ respectively.

Also as before, let’s consult our definitions! By definition, because $M, N$ are both odd, we can again write $M = 2k+1$ and $N = 2l+1$ , for two integers $k, l$ .

Therefore, $M \cdot N = (2k+1) \cdot (2l+1)$ . Expanding this product gives you $4kl + 2k + 2l + 1$ , which you can regroup as $(4kl+ 2k + 2l) + 1$ . Factoring a 2 out of the left-hand part gives you $2(2kl + k + l) + 1$ .

Because $k, l$ are integers, the expression $2kl + k + l$ inside the parentheses is an integer as well, as any product or sum of integers is still an integer. Therefore, we’ve written $M \cdot N$ in the form $2 \cdot (\text{an integer}) + 1$ ; i.e. we’ve shown that $M \cdot N$ satisfies the definition of being an odd integer! $\Box$

Proof.

As before, let’s start by working in general. Take any integer $N$ .

As a thought experiment, let’s think about what it would mean for $N$ to be both odd and even at the same time.

If $N$ was even, then by definition we could write $N = 2k$ for some integer $k$ ; as well, if $N$ is also odd, then by definition we should be able to write $N = 2l + 1$ for some integer $l$ .

Note that we had to pick different letters $k, l$ when we applied the even and odd definitions! If we had used the same letter $k$ for both, that would imply that the same integer is being used in both definitions, and this might not be true.

As a result, we have $N = 2k$ and $N = 2l+1$ . Combining gives us $2k=2l+1$ , which we can rearrange into $2(k-l) = 1$ ; i.e. $k-l = \frac12$ .

But this is clearly not possible! $k$ and $l$ are both integers, and so their difference must an integer as well; it cannot be $\frac12$ !

As a result, we’ve shown that it is impossible for an integer $N$ to be equal to $2k$ and $2l+1$ at the same time if $k, l$ are both integers; that is, it is impossible for $N$ to be both odd and even! $\Box$

By definition, you can think of our even/odd split above as classifying every number as either “a multiple by 2” or “not a multiple of 2.” We expand on this idea in the following section, where we study divisibility and prime numbers.

Divisibility and Primes

There are many synonyms for “divides”: each of the phrases

• ”$a$ is a divisor of $b$ “,
• ”$a$ is a factor of $b$ “,
• ”$b$ is a multiple of $a$ “,
• ”$b$ can be divided by $a$ ,” and
• $a \mid b$

all mean the same thing as ”$a$ divides $b$ .”

Here’s a string of examples, to make this clearer:

Example 1.3.

• $4$ divides $12$ ; this is because we can multiply 4 by 3 to get 12.
• $72$ can be divided by $-6$ ; this is because we can multiply $-6$ by $-12$ to get 72.
• $2$ does not divide $15$ ; this is because for any integer $k$ , $2k$ is an even number, and so is in particular never equal to an odd integer like 15.
• $n$ is a multiple of $1$ for any integer $n$ ; this is because we can always multiply 1 by $n$ to get $n$ .
• $n$ is a factor of $0$ for any integer $n$ ; this is because we can always multiply $n$ by 0 to get 0.

Example 1.4. Note that the phrases “divides” and “can be divided by,” while quite similar-sounding in English, have almost the opposite meaning in mathematics! For instance, 3 divides 9 and 9 can be divided by 3 are the same claims.

To get some practice with making abstract arguments about divisibility, let’s study a simple claim about factors and divisibility:

Again, we need to work in abstract! That is: we cannot just check this for a few values and say that “well, when $a=4, b=12, c=36$ this all works out.” Instead, we must consider any three integers $a,b,c$ , and work in general without knowing what $a,b,c$ are.

By definition, if $a$ divides $b$ , we can write $ak = b$ for some integer $k$ . Similarly, if $b$ divides $c$ , then we can write $bl = c$ for some integer $l$ .

Now, take the equation $ak=b$ , and use this to substitute in $ak$ for $b$ in our second equation $bl=c$ . This gives us $akl = c$ , i.e. $a(kl) = c$ . Because $k, l$ are both integers, their product is an integer; as a result, we’ve written $a \cdot (\textit{an integer}) = c$ . In other words, by definition we have shown that $a$ is a factor of $c$ , as desired.

A particularly useful concept related to divisibility is the concept of a prime number:

Example 1.5. The first few prime numbers are $2,3,5,7,11,13,17,19,23,29, \ldots$

Proof.

This is because 1’s only factor is 1, and so 1 does not have two distinct positive integer factors.

Proof.

This is because every other positive even number by definition has the form $2k$ , and so has at least $1,2,k, 2k$ as its set of factors (and thus has more than 2 distinct positive factors.)

Example 1.6. $6 = 2 \cdot 3$ , $9 = 3 \cdot 3$ , and $24 = 2 \cdot 12$ are all composite.

Example 1.7. Here are a few prime factorizations:

• $120 = 2^3\cdot 3 \cdot 5$ ,
• $243 = 3^5$ ,
• $30031 = 59 \cdot 509$

Here are a pair of useful observations about prime numbers:

Theorem 1.1. Every positive integer can be factorized into a product of prime numbers in exactly one way, up to the ordering of those prime factors.

In other words, this theorem is saying the following:

• Every positive integer can be factored into primes, as illustrated above. So, for example, we can take 60 and write it as $2 \cdot 2 \cdot 3 \cdot 5$ .

• No number can be factored into primes in two different ways, up to the ordering. That is: while you could write $60$ as $5 \cdot 2 \cdot 3 \cdot 2$ or $5 \cdot 3 \cdot 2 \cdot 2$ , you’re never going to write a prime factorization of 60 that has a 7 as one of its prime factors, or doesn’t have a 5.

Proving this theorem is a bit beyond our skill set at the moment. Instead, let’s mention a second useful fact about primes:

Theorem 1.2. There are infinitely many primes.

This proof is also a bit beyond us for now. However, if you skip ahead to the proof by contradiction section of our notes / wait a few weeks, you’ll see a proof of this in our course!

Prime numbers (as you’ll see in Compsci 110) are incredibly useful for communicating securely. Using processes like the RSA cryptosystem, one of the first public-key cryptosystems to be developed, you can use prime numbers to communicate secretly over public channels.

Prime numbers are also quite baffling objects, in that despite having studied them since at least 300 BC there are still so many things we do not know about them! Here are a few particularly outstanding problems, the solutions for which would earn you an instant Ph.D/professorship basically anywhere you like in the world:

In general, working with prime numbers can get tricky very fast; even simple problems can get out of hand! With that said, there are some claims that are approachable. We study two such statements here:

Proof.

As noted before, examples alone aren’t enough for a solution. However, if you’re stuck (as many of us would be on first seeing a problem like this) they can be useful for helping us find a place to start!

So: let’s create a bunch of two-digit numbers and factor them (say, via WolframAlpha.) If our claim is wrong, then maybe we’ll stumble across a number whose only factors are 1 and itself. Conversely, if our claim is right, maybe we’ll see a pattern we can generalize! We do this at right.

As we do this, a pattern quickly emerges: it looks like all of these numbers are multiples of 101! This isn’t a solution yet: we just checked six numbers out of quite a few possibilities. It does, however, tell us how to write a proper argument here:

Notice that for any two-digit number $ab$ , $ab \cdot101 = ab \cdot 100 + ab = ab00 + ab = abab$ . Therefore, any number of the form $abab$ is a multiple of 101 and also a multiple of $ab$ , by definition. Because $ab$ is a two-digit number by definition, this means that $abab$ has at least two factors other than 1. This means that $abab$ cannot be a prime number, as claimed! $\Box$

Proof.

We use the “suppose we’re wrong” technique from Claim 1.3. That is: take any number $n$ with the “no factors in the set $2,3,\ldots k$ ” property listed above. There are two possibilities:

• $n$ is prime. This is what we want: if this case holds, we’re done!

• $n$ is not prime. We want to show that this case cannot hold; if we can do this, then we are left with only the case above, and have thus proven our claim!

  To do this: note that if $n$ is not prime, then, it must have more than 2 factors. Let $a$ be one of those positive factors that is not $1$ or $n$ ; by the definition of factor, then, we can write $n = ab$ for some positive integer $b$ , and thus have that $b$ is also another factor of $n$ .

  We know that because $a \neq n$ that $b \neq 1$ . We also know that because both $a,b$ are factors of $n$ , that by our “suppose we’re wrong” assumption that $a,b \neq 2,3,4,\ldots k$ . Therefore, by combining these results, both $a,b > k$ ; that is, both $a,b$ are greater than $\sqrt{n}$ .

  But this means that $ab > \sqrt{n} \cdot \sqrt{n} = n$ . But this is impossible, as $ab= n$ .

Therefore the only possibility left is that $n$ is prime, as desired. $\Box$

This last claim is particularly useful! We know that by definition, a positive integer $n$ is prime if it has exactly two positive integer factors: 1 and itself. Naively, then, to check if a number $n$ is a prime, you might think that you would have to check all of the numbers $2,3,4,\ldots n-1$ each individually, and see if any of them divide $n$ .

However, Claim 1.6. tells us that we don’t actually have to check all the numbers up to $n-1$ ; we only have to go up to $\sqrt{n}$ . This can save us a lot of time: as you’ll see later in this coursebook in our runtime-analysis section / in papers like Compsci 130 and 220, a “runtime” of checking $\sqrt{n}$ cases is considerably better than a “runtime” of checking $n$ cases!

For instance, to see if $n=101$ is prime, Claim 1.6. tells us that because 101 is not a multiple of 2,3,4,5,6,7,8,9 or 10, then 101 is itself a prime. (Much faster than checking all of the numbers up to 100.)

We leave a few more exercises along these lines for the end of this chapter. For now, we turn to an extension of the ideas behind divisibility: modular arithmetic!

Modular Arithmetic

Modular arithmetic is something you’ve been working with since you were a child! Specifically, think about how you tell and measure time:

• Suppose that it is currently 6am and 3 hours pass. Because $6+3 = 9$ , we know that the answer is 9am.

  Now, suppose that it is 11am and 18 hours pass. What is the time now? Unlike the process above, you would not find the answer here by adding 18 to 11 and getting “29 o’clock.” Instead, you’d find $11+18 = 29$ , and then subtract off 24 to get the right answer, $\fbox{5 am}$ . In general, when you’re adding hours together to tell time, you do so on a circle (as drawn at right,) where measurements “wrap around” every 12 hours. That is: if it is 7 o’clock now and 38 hours pass, then the hour hand on a clock would point to a 9; this is because $7+36 = 45$ , and $45 - 12 - 12 - 12 = 9$ .

• In the above example, we saw that hours wrapped around in units of 12. Similarly, we know that days of the week repeat in groups of 7. That is: let Monday = 0, Tuesday = 1, and so on/so forth until we get to Sunday = 6. Then, suppose that it is Thursday and we want to know what day of the week it is in 10 days. We can see that because “Thursday $+10$ ”$= 3+10 = 13$ and $13-7 = 6$ , the day must be Sunday.

• Similarly, seconds wrap around in groups of 60. That is: if you type in “99” on your microwave and walk away, the same amount of time passes as if you had entered “1:39”, because $99 - 60 = 39$ and thus 99 seconds is a minute and 39 seconds.

All of these calculations involved arithmetic where our numbers “wrapped around” once they got past a certain point. This idea is the basis for modular arithmetic, which is arguably the most useful mathematical concept you’ll encounter in computer science.

To make this rigorous, let’s make a definition:

• If $a \geq n$ , repeatedly subtract $n$ from $a$ until $a < n$ . The result of this process is $a \% n$ .
• If $a < 0$ , repeatedly add $n$ to $a$ until $a \geq 0$ . The result of this process is $a \% n$ .

• If neither of these cases apply, then by definition $0 \leq a < n$ . In this case, $a \% n$ is simply $a$ (that is, we don’t have to do anything!)

We call $\%$ the modulus operator. Most programming languages implement it as described here, though (as always) you should read the documentation for details.

To get a handle on this, we calculate a number of examples:

Example 1.8.

• $6 \% 2 = 0$ . To see why, simply run the process above. Because $4 > 2$ , we just subtract copies of 2 from 4 until we get something less than 2: $6 \xrightarrow{\textrm{subtract }2} 4 \xrightarrow{\textrm{subtract }2} 2 \xrightarrow{\textrm{subtract }2} \boxed{0}$ .

• $-9 \% 2 = 1$ . To see why, simply run the process above. Because $-9 < 0$ , we just add copies of 2 from 4 until we get something nonnegative: $-9 \xrightarrow{\textrm{add }2} -7 \xrightarrow{\textrm{add }2} -5 \xrightarrow{\textrm{add }2} -3 \xrightarrow{\textrm{add }2} -1 \xrightarrow{\textrm{add }2}\boxed{1}$ .

• In general, if $n$ is any even number, then $n \% 2 = 0$ . This is because if we start with any even number $n = 2k$ , the process above will reduce $2k$ to 0 after subtracting/adding $2$ $k$ times in a row.

• Similarly, if $n$ is any odd number, then $n \% 2 = 1$ . These two observations come in handy when working with binary arithmetic: as you’ll see in Compsci 110, these facts tell you that you can tell if a number is even or odd by looking at its last digit in binary!

• $3 \% 4 = 3$ . This is an easy one to calculate: because $0 \leq 3 < 4$ , we don’t have to do anything here!

We also study a quick argument-based problem, to make sure that we’re comfortable with a more “abstract” way of working with the modulus operator $\%$ :

Proof.

As always, because this is a claim about any two integers, we need to work in general. That is: we cannot pick examples for $a$ and $n$ , and instead need to consider every possible pair of values for $a, n$ with $n > 0$ .

Our algorithm had three different cases: one for when $a \geq n$ , one for when $a < 0$ , and one for when $0 \leq a < n$ . As such, our argument will likely want three cases as well:

• $a \geq n$ . In this case, our algorithm repeatedly subtracted copies of $n$ from $a$ until it got to something less than $n$ .

  This process clearly only runs for finitely many steps, as $a$ starts off as greater than $n$ and decreases by a fixed nonzero amount at each step. In particular, it must eventually be less than $n$ , as that was the condition we gave for this process to stop.

  As well, if $a \geq n$ , then $a-n \geq 0$ ; as a result, when this process ends, it cannot end at a negative number.

  Therefore, at the end of our process we’ve reduced $a$ so that it’s nonnegative and less than $n$ , as desired.

• $a < 0$ . In this case, our algorithm repeatedly added copies of $n$ from $a$ until it got to something positive.

  As before, this process clearly only runs for finitely many steps; this is because $a$ starts off as a negative number and increases by a fixed amount at each step. In particular, it must eventually be nonnegative, as that was the condition we gave for this process to stop.

  As well, if $a < 0$ , then $a+n < n$ ; as a result, when this process ends, it cannot end at a value equal to or greater than $n$ .

  Therefore, at the end of our process we’ve reduced $a$ so that it’s nonnegative and less than $n$ , again as desired.

• $0 \leq a < n$ . In this case our algorithm just outputs $a$ , which again has the desired properties.

Because every integer $a$ falls into one of these three cases, we’ve proven our claim for all values of $a$ and all $n > 0$ , as desired. $\Box$

This sort of argument (that a given algorithm “works”) is one that we will make repeatedly in this class! More generally, these are the most common sorts of arguments you’ll want to make in computer science: when working with any problems that require nontrivial algorithms or thought, you’ll often want to be able to write proofs that the process should be bug-free in theory.

Modular arithmetic comes up often in computer science and mathematics:

• Remainders. Take any two positive integers $a, b$ . We say that the quotient of $a$ on division by $b$ is just ”$\frac{a}{b}$ rounded down:” that is, we say that the quotient of $\frac{14}{3}$ is 4, as $\frac{14}{3} = 4.66666\ldots$ rounds down to 4.

  Based on this, we say that the remainder of $\frac{a}{b}$ is the difference of $a$ and the quotient of $a$ on division by $b$ times $b$ ; that is, the remainder of $\frac{a}{b}$ is everything “left over” after we try to divide through by $b$ .

  Notice that by definition, $a \% b$ is the remainder of $\frac{a}{b}$ ! So, for example, we have the following:

  • Because $14 \% 12 = 2$ , we have that the remainder of $\frac{14}{12}$ is 2.

  • Because $26 \% 13 = 0$ , we have that the remainder of $\frac{26}{13}$ is 0.

• Binary arithmetic. Computers are built off of the binary number system: i.e. instead of storing numbers in decimal notation where we use the digits 0,1,2,\ldots 9, computers store everything with just 0’s and 1’s (i.e. on and off, which computers are much better at storing than something as imprecise as a decimal digit!) To work with numbers in binary, we often work modulo 2, as you’ll see in classes like Compsci 110.

• Overflow errors. In many programming languages, you have to tell the computer the “type” of any variable that you want to work with. That is, you can’t just tell the computer that x = 3;” instead, you have to first tell the computer that $x$ is an integer by writing something like ”int x;” and then say ”x = 3.”

  However, when you declare that $x$ is an integer, your computer does not automatically assume that $x$ can literally be any integer! This is because when a computer declares a variable, it typically has to set aside a block of space to store the information corresponding to that variable. As a result, the computer has to make an assumption about a reasonable range of values that your integer will fall between (a common range is $-2^{31}$ to $2^{31} - 1$ , i.e. you use 32 bits to describe your integer in binary, with one of those used to record $\pm$ .)

  Suppose you did this, though, and later on tried to increase the value stored in $x$ past its maximum value: i.e. you had $x = 2^{31}-1$ , and you tried to add one to $x$ . The result (if you ignore warnings / errors produced by your compiler) won’t be $2^{31}$ , because this value is too large to store! Instead, it will often “overflow” and wrap around to become $-2^{31}$ instead. That is: computers technically do a lot of their arithmetic “mod $2^{32}$ ,” and this can trip you up if you’re not being careful about the sizes of your variables! Check out Wikipedia’s integer overflow page for a bunch of examples and discussion around how to handle this situation.

• Checksums. On almost every ID number or tag (i.e. barcodes, bank account numbers, library book numbers, etc) the last digit or two is a “checksum” digit, found by adding up the previous numbers and applying the $\% n$ operator to the result (with $n$ usually being 10, but sometimes something stranger like 97 in the case of bank account numbers.)

  The use of these checksum digits is that they let a computer program spot typos: if someone makes a mistake when entering a number, they’ll usually do so in a way that changes the modulus of the sum! As a result, we can spot this error by rechecking the modulus, and alert the user that they’ve made a mistake.

• Cryptography. Calculating remainders modulo $n$ has been key to the entire field of cryptography, from its inception in ancient Rome to its present-day uses. There is almost no way to keep information secret in the modern world that does not use modular arithmetic in some way.

  As an example, let’s look at how modular arithmetic is used in one of the first forms of cryptography: the Caesar cipher, otherwise known as a shift cipher!

  • To set this up, take the alphabet $\{a,b,\ldots z\},$ and label each letter with the numbers $\{0,1,\ldots 25\}$ , as shown at right. Also choose a secret key $k$ from the set of numbers $\{0,1,\ldots 25\}$ ; for this problem, let’s pick our secret key to be $k=15$ .

  $a$

  $b$

  $c$

  $d$

  $e$

  $f$

  $g$

  $h$

  $i$

  $j$

  $k$

  $l$

  $m$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $0$

  $1$

  $2$

  $3$

  $4$

  $5$

  $6$

  $7$

  $8$

  $9$

  $10$

  $11$

  $12$

  $n$

  $o$

  $p$

  $q$

  $r$

  $s$

  $t$

  $u$

  $v$

  $w$

  $x$

  $y$

  $z$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $\downarrow$

  $13$

  $14$

  $15$

  $16$

  $17$

  $18$

  $19$

  $20$

  $21$

  $22$

  $23$

  $24$

  $25$

  • Now, take the message you want to send: for example, let’s send the phrase $\fbox{chain fusion}$ .

  • Swap the letters for numbers, to get $\fbox{2.7.0.8.13~~5.20.18.8.14.13}$ .

  • Take each number in your code and add our secret code to it: this gives us $\fbox{17.22.15.23.28~~20.35.33.23.29.28}$ .

  • Now replace each number in our code with its value modulo 26; this gives us $\fbox{17.22.15.23.2~~20.9.7.23.3.2}$ .

  • Translate this back to letters, to get the encrypted message $\fbox{rwpxc ujhxdc}$ . To an outsider, this would look like gibberish! In ancient Roman times, most people who would intercept such a message would assume that it was written in a foreign language and not be able to translate it.

  • But, if you knew the secret key, you could just translate this message back to numbers and subtract 15 from each letter modulo 26. This would give you the original message, as desired.

This specific cipher is easy to crack: a simple brute-force approach of trying all 26 keys one-by-one on the encrypted text would lead you to the right answer pretty quickly. (Try it out by hand or by writing a program; it’s not too bad.)

There are better ways to keep information secure, though! See courses like Compsci 110 and Maths 328 for some more modern approaches (that still use modular arithmetic at their core!)

% and Arithmetic

Question 1. What is $12345678910111213141516171819^{12345678910111213141516171819}$ ?

If you tried to use a computer to directly expand this problem, the size of the resulting number (approximately $10^{10^{29}}$ ) would take up $\approx 10^{17}$ terabytes, i.e. several orders of magnitude in excess of the current total storage capacity of humanity.

And yet, if you pop over to WolframAlpha and ask it this question, you’ll get the following answer in about three seconds:

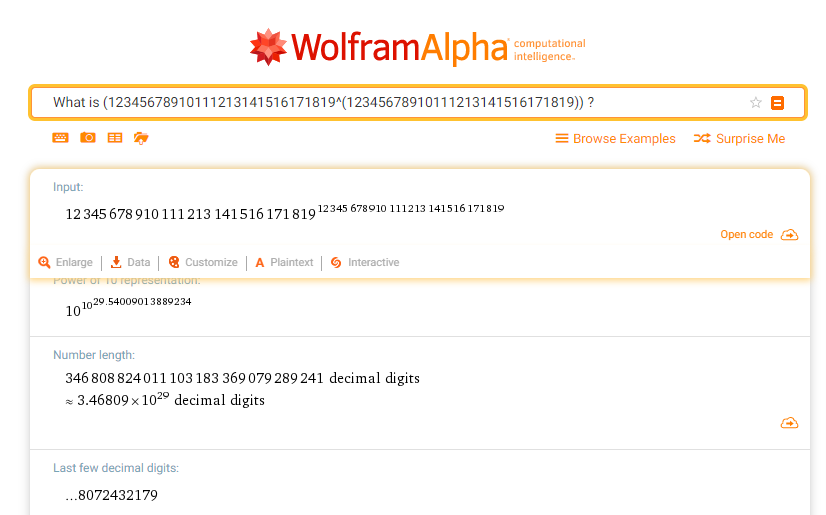
So: how is WolframAlpha able to calculate this so quickly, if the precise result is so staggeringly huge?

Partly, this is because the “powers-of-ten” approximation can be made by replacing the values here with just large powers of 10: i.e. things like $12345678910111213141516171819 \approx 10^{28}$ can make approximating things a bit easier. However, WolframAlpha also seems to know the last few digits of this number, which seems a little bit spooky: how can you calculate this without understanding the entire number?

The trick here is the modulus operation, which we can use to perform certain arithmetic tasks very quickly. To show how this is possible, we introduce the closely related idea of congruency modulo $n$ :

To get an idea for how this works, we calculate a number of examples here:

Example 1.9.

• $21 \equiv 5 \mod 8$ ; this is because $21-5 = 16 = 2 \cdot 8$ is a multiple of 8.
• $21 \equiv 13 \mod 8$ ; this is because $21 - 13 = 8$ is a multiple of 8. Notice that it’s possible for a number to be congruent to many other possible values: i.e. 21 was congruent to both 5 and 13 modulo 8!
• $-19 \equiv 7 \mod 2$ ; this is because $-19 - 7 = -26 =(-13) \cdot 2$ is a multiple of 2.
• $14 \not\equiv 18 \mod 5$ ; this is because $14 - 18 = -4$ is not a multiple of 5.
• For any two integers $a,b$ , $a \equiv b \mod 1$ ; this is because $a-b$ is always a multiple of 1 (as any integer is a multiple of 1!)
• For any two integers $a,b$ , we have $a \equiv b \mod 2$ if and only if $a,b$ are both even or $a,b$ are both odd. This is because $a\equiv b \mod 2$ holds if and only if $a-b$ is a multiple of 2, i.e. $a-b$ is even, and this only happens when $a,b$ are the same parity: i.e. when they’re both even or both odd.

Congruency and our modulus operator are very closely linked:

We reserve proving this claim for your practice problems at the end of this chapter (see exercise 7). Instead, let’s talk about how we can use this:

This claim is basically just saying that we can do “arithmetic modulo $n$ !” That is: for numbers $a,b,c,d$ , you know that if $a=b, c=d$ then $ac=bd$ and $a+c = b+d$ , by just combining these equalities with the addition and multiplication operations. This claim is saying that if your values are “equal modulo $n$ ,” the same tricks work!

We prove this claim here:

Proof.

We need to prove our claim in general here, as we’re making a claim about any possible set of values, not a specific set of values! To do so, we let $a,b,c,d,n$ be any set of integers such that $a \% n = b \% n$ and $c \% n = d \% n$ .

If we now use Claim 1.8, we get the following: $a-b$ is a multiple of $n$ , and $c-d$ is a multiple of $n$ . By definition, this means that we can write $a-b = kn$ and $c-d = ln$ for some pair of integers $k, l$ .

By adding these equations together, we get $(a+c)-(b+d) = kn+ln = (k+l)n$ ; that is, that $(a+c)-(b+d)$ is a multiple of $n$ . This means that, by Definition 1.8, $a+c \equiv b+d \mod n$ ! Applying Claim 1.8 gives us $(a+c) \% n = (b+d) \% n$ , as claimed.

If we take $a-b = kn$ and multiply both sides by $c$ , we get $ac - bc = kcn$ ; similarly, if we take $c-d = ln$ and multiply by $b$ we get $bc-bd = bln$ . Adding these equations together gives us $ac-bc+bc-bd= kcn+bln = (kc+bl)n$ ; i.e. $ac-bd$ is a multiple of $n$ . This means that $ac \equiv bd \mod n$ ! Again, applying Claim 1.8 then tells us that $(ac) \% n = (bd) \% n$ , as desired.

A quick corollary to Claim 1.9 is the following:

Corollary 1.1. If $a\%n = b\% n$ , then for any positive integer $k$ , we have $(a^k) \% n = (b^k) \% n$ .

We leave proving this for Exercise 9; try proving this by using the multiplication property in Claim 1.9!

Instead of spending more time with this sort of abstract stuff, let’s do something practical: let’s talk about how we could solve our WolframAlpha problem! Specifically, let’s solve the following problem:

Proof.

The clever thing here is not that we can calculate this (again, if we just wanted an answer, we could plug this into WolframAlpha), but rather that we can calculate this easily! That is: we can use modular arithmetic to find this number without needing a calculator, with relatively little work overall.

To do so, just make the following observations:

• First, $213047 \% 10 = 7$ , and in general any positive number is congruent to its last digit modulo 10. This is by definition: if you take any number $a$ greater than 10, subtracting 10 from it does not change its last digit! Therefore, the process we defined to calculate $a\% 10$ will never change the last digit of $a$ , and thus its output at the end is precisely $a$ ’s last digit.

• Therefore, we have that $\left(213047^{129314}\right) \% 10 = \left(7^{129314}\right) \% 10$ , by using our “exponentiation” result from earlier.

• Now, notice that $\left(7^2\right) \% 10 = 49 \% 10 = 9$ , and thus that $\left(7^4\right) \% 10 = \left(7^2 \cdot 7^2\right) \% 10 = (9 \cdot 9) \% 10 = 81 \% 10 = 1$ .

  As a result, we have that for any $k$ , $\left(7^{4k}\right) \% 10 = (7^4)^k \% 10 \equiv 1^k \% 10 =1.$

• Therefore, because $129314 = 129300 + 12 + 2$ , and any multiple of 100 is a multiple of 4, we have that $\left(7^{129314}\right) \% 10 = \left(7^2 \cdot 7^{\textrm{a multiple of 4}} \right) \% 10 = 9 \cdot 1= 9$ .

In other words, our number’s last digit is $\boxed{9}$ !

It’s worth noting that this trick isn’t just useful for humans, but for computers as well: you can use tricks like this to massively speed up calculations in which you only care about the number’s last few digits, and/or other pieces of partial information.

We can use this trick to basically calculate any number to any other number’s last digit! For example, the task of finding the last digit of

is now something we can do very quickly:

• Like before, we only care about the last digit of the thing we’re exponentiating: i.e. we can reduce this problem to just finding $9^{123\ldots19}$ ’s last digit.
• $\left( 9^2\right) \% 10 = 81 \% 10 = 1$ ; therefore, for any even number $2k$ , we have $\left(9^{2k}\right) \% 10 = \left((9^2)^k\right) \% 10 = 1^k = 1$ .
• Therefore, for any odd number $2k+1$ , we have $\left( 9^{2k+1}\right) \% 10 = \left( 9 \cdot 9^{2k}\right) \% 10 = 9 \cdot 1 =9$ .
• So, because the last digit of our base is 9 and the exponent is odd, the last digit of our entire number is $\boxed{9}$ !

Generalizations of this process (i.e. working modulo 100 to find the last two digits, etc) can be used to quickly find the last few digits of any number. This can be quite useful when writing computer algorithms: most of the time when working with large numbers, you only need the first few and last digits for an approximation of its size, not the entire exact value!

Other Number Systems

In the past five sections, we’ve focused on studying the integers; i.e. whole numbers. However, there are lots of problems in real life whose answers cannot be given with just integers alone. Even going back to primary school, you’ve seen and solved problems like the following:

• Suppose that three hedgehogs come across two sausages while wandering through a backyard barbie, and want to share them equally. How many sausages should each hedgehog get?
• If you have one and a half pavlovas left over from the barbeque, and you eat a third of one for breakfast, how much pav do you have left?

• How many dollars are there in ten cents?

The answers to each of these $\left(\frac23, \frac32 - \frac13 = \frac76\textrm{ and }\frac{10}{100} = \frac{1}{10}\textrm{, respectively}\right)$ are all relatively easy to calculate, and are tasks you’ve seen in school for years now! However, their solutions are not things that we can express as integers.

To work with them, we need some new sets of numbers! We start with one such set that you’re already familiar with: